Unit 6 worksheet 2 finding coterminal angles – Embark on a mathematical journey with Unit 6 Worksheet 2: Finding Coterminal Angles, where we unravel the intricacies of angles that share a terminal side. Prepare to delve into a world of degrees and radians, discovering the methods, applications, and special cases of coterminal angles.
Coterminal angles, with their captivating relationship and shared terminal side, provide a gateway to simplifying trigonometric calculations and unlocking real-world applications. Join us as we explore the fascinating world of coterminal angles, equipping you with the knowledge and skills to conquer any angle-related challenge.
Coterminal Angles: Definition and Overview

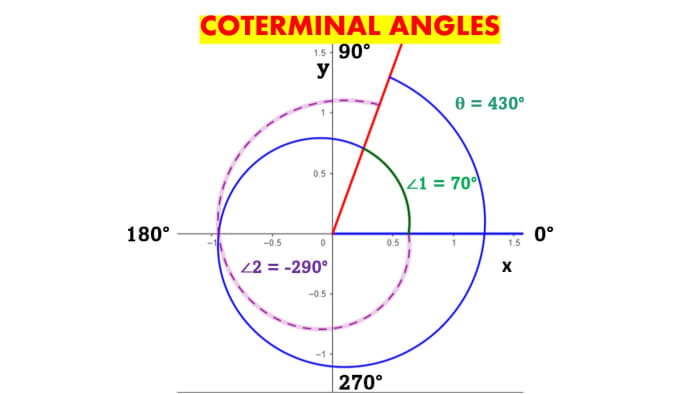
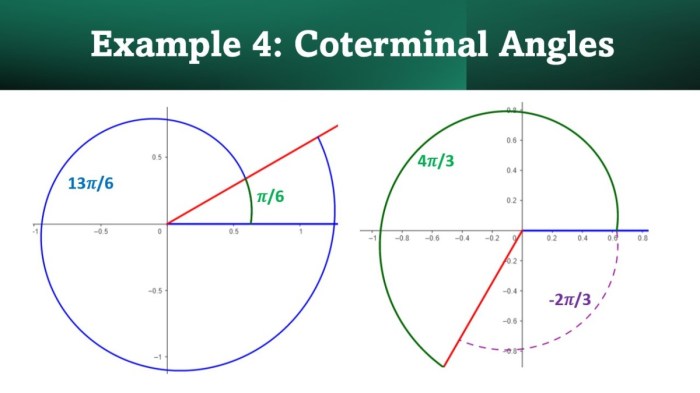
Coterminal angles are angles that share the same terminal side. In other words, they have the same ending point on the unit circle. Coterminal angles can be found by adding or subtracting multiples of 360 degrees (or 2π radians) to a given angle.
For example, 30 degrees and 390 degrees are coterminal angles because they both have the same terminal side. Similarly, -30 degrees and 330 degrees are coterminal angles because they also have the same terminal side.
Methods for Finding Coterminal Angles
There are two main methods for finding coterminal angles:
- Add or subtract 360 degrees (or 2π radians) to the given angle.
- Find the angle’s coterminal angle in the interval [0, 360) degrees (or [0, 2π) radians].
To use the first method, simply add or subtract 360 degrees (or 2π radians) to the given angle until you get an angle that is within the interval [0, 360) degrees (or [0, 2π) radians). For example, to find the coterminal angle of 450 degrees, we can subtract 360 degrees to get 90 degrees.
To use the second method, first find the quadrant in which the given angle lies. Then, subtract or add the appropriate number of degrees (or radians) to get an angle that is in the interval [0, 360) degrees (or [0, 2π) radians).
For example, to find the coterminal angle of 450 degrees, we can subtract 360 degrees to get 90 degrees. Since 90 degrees is in the first quadrant, it is the coterminal angle of 450 degrees.
Special Cases and Exceptions
There are two special cases to consider when finding coterminal angles:
- Angles that are multiples of 360 degrees (or 2π radians) are coterminal with themselves.
- Angles that are greater than 360 degrees (or 2π radians) can be found by subtracting 360 degrees (or 2π radians) until you get an angle that is within the interval [0, 360) degrees (or [0, 2π) radians).
For example, 360 degrees is coterminal with itself because it has the same terminal side as 0 degrees. Similarly, 720 degrees is coterminal with 0 degrees because it can be found by subtracting 360 degrees from 720 degrees.
Applications of Coterminal Angles, Unit 6 worksheet 2 finding coterminal angles
Coterminal angles are used in a variety of applications, including trigonometry and navigation.
In trigonometry, coterminal angles are used to simplify calculations. For example, the sine of 30 degrees is the same as the sine of 390 degrees because they are coterminal angles.
In navigation, coterminal angles are used to find the direction of a ship or aircraft. For example, a ship that is traveling at a heading of 450 degrees is traveling in the same direction as a ship that is traveling at a heading of 90 degrees because they are coterminal angles.
Interactive Examples and Practice
To practice finding coterminal angles, try the following interactive examples:
You can also practice finding coterminal angles by solving the following problems:
- Find the coterminal angle of 45 degrees.
- Find the coterminal angle of
30 degrees.
- Find the coterminal angle of 540 degrees.
Answers to the practice problems:
- 45 degrees
- 330 degrees
- 180 degrees
FAQ Resource: Unit 6 Worksheet 2 Finding Coterminal Angles
What is the definition of coterminal angles?
Coterminal angles are angles that share the same terminal side.
How do I find coterminal angles?
To find coterminal angles, add or subtract 360 degrees (or 2π radians) to the given angle.
What are some applications of coterminal angles?
Coterminal angles are used in trigonometry to simplify calculations and solve real-world problems involving angles.